top of page

RESEARCH

Much of my research takes an interdisciplinary approach to collaboration, where I use mathematical, statistical, and computational methods to answer epidemiological questions about non-infectious diseases.

​

I am keenly interested in the structural differences between models of infectious disease and those of substance use disorders, and how they give rise to the need for new mathematical analyses.  My dissertation is primarily focused on how substance abuse and subsequent addiction develops in a population, and how mathematics can shed light on the nuances of these diseases.

​

Outside of substance use epidemiology, I perform research using statistical modeling to analyze data collected from a 2-year, multi-site longitudinal study on late-life depression (LLD). We are examining the effect of both white matter hyper- and hypointensities, which are markers of vascular depression, on depression recurrence for individuals with remitted LLD.

SIR.png

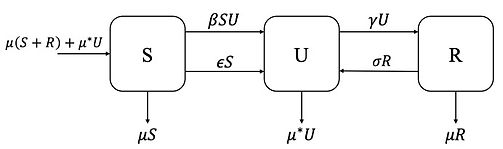
Compartmental diagrams for the classic SIR infectious disease model a general SUD model I created and analyzed using optimal control.  Both models assume that each class represents a proportion of the total population (N=1) and increased death due to infection or addiction.  The SIR model assumes immunity from reinfection while the SUR model allows for relapse.  Most notably, the SUR model allows for SUD to develop without social contact/influence through the pathway ɛS.  This linear perturbation away from SIR causes drastic changes in dynamics, shown below.

Numerical depictions of the dynamical shift caused by the addition of the linear addiction rate ɛS into an SIR-like framework.  Note, when ɛ = 0, there exists both a use disorder-free equilibrium (UDFE) and an endemic equilibrium that change stability at the bifurcation point, namely R_0 = 1 where R_0 is the basic reproductive number.  When this model is perturbed by letting ɛ > 0, the bifurcation point no longer exists and the model produces only one feasible equilibrium that is strictly positive and globally (asymptotically) stable.

SUS_bifurcation_plots.png

Upcoming Publications

  • Pearcy, Karim, Butters, Krafty, Boyd, Banihashemi, Szymkowicz, Hassenstab, Landman, Ajilore, Taylor, Andreescu. “White matter hyperintensities and relapse risk in late-life depression.” In review at the American Journal of Geriatric Psychiatry.

  • Pearcy*, Queen*, Jodoin, Lenhart, Strickland.  "Construction and Data-driven Analysis of a Stochastic, Individual-based Opioid Epidemiology Network Model."  In preparation. (* indicates shared first authorship)

  • Pearcy, Hong, Rayson, Bland, Rosen. “Regional Modeling of Supply Chain Resiliency Across Industries through Ordinary Differential Equation Modeling.”  In preparation.​

Publications

bottom of page